Biscotti Danesi Danish Cookies // Småkager: Numbers? Natural :P

What are natural numbers? How do define them? How can they be visualized "graphically"?

1- Peano defines numbers like this:
0 is a natural number
...
For every natural number n, S(n) is a natural number.
...
The set of natural numbers is then defined as: N = {0, S(0), S(S(0)), …}

NOTE: S(n) is basically n+1

2- S(n) has interesting properties:
$\begin{align} a + 0 &= a ,\\ a + S (b) &= S (a + b). \end{align}$
and
$\begin{align} a \cdot 0 &= 0, \\ a \cdot S (b) &= a + (a \cdot b). \end{align}$

3- It is possible to define natural numbers using only sets:
s(a) = a ∪ { a }

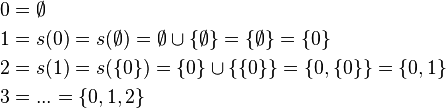
$\begin{align} 0 &= \emptyset \\ 1 &= s(0) = s(\emptyset) = \emptyset \cup \{ \emptyset \} = \{ \emptyset \} = \{ 0 \} \\ 2 &= s(1) = s(\{ 0 \}) = \{ 0 \} \cup \{ \{ 0 \} \} = \{ 0 , \{ 0 \} \} = \{ 0, 1 \} \\ 3 &= ... = \{ 0, 1, 2 \} \end{align}$

Visually it could be: 0 = [] "zero is a box"
and: S( [a] ) = [ a [a] ]

So: [] -> S([]) = [[]] -> S(S([])) = [ [] [[]] ] -> ...

4- Another way to visualize natural numbers is to use a string:
Z for zero
S for S(.), and S(Z) = SZ is one

So N = { Z, SZ , SSZ , SSSZ , ... }
This basically is the unary system, only that a special symbol is used ("Z" here) to mark the beginning of the string representing a number. (this offers advantages when using a Turing Machine or lambda calculus to define arithmetic operators).

5- Since each natural number can be expressed in a unique way by its prime factors (up to sorting), it is possible to define a diagram for each natural number, as they do here; these diagrams are also described here:

They are nice and prime numbers can be recognized because they are circles! But the diagrams tend to be large an less interesting for natural numbers with large factors.

6- Gödel numbering: a way to encode a list of numbers into a single (LARGE) one, so that it is always possible to re-compute back the original list of numbers.
The idea is:
$\mathrm{enc}(x_1,x_2,x_3,\dots,x_n) = 2^{x_1}\cdot 3^{x_2}\cdot 5^{x_3}\cdots p_n^{x_n}.\,$
where p_n is some prime.

Example: the list (1,2,3) can be encoded as the number 2¹ * 3²* 5³= 2*9*125 = 750
Since 2, 3 and 5 are the first 3 primes. To de-code the list, simply use the fundamental theorem of arithmetic, and find the prime factors of 750:
750 = 2¹ * 3²* 5³
then be sure that the primes are sorted from smaller to larger, and read the exponents: (1,2,3) et voila' :)